Topological orderings

Exercises 5.12 and 5.13 and 5.14

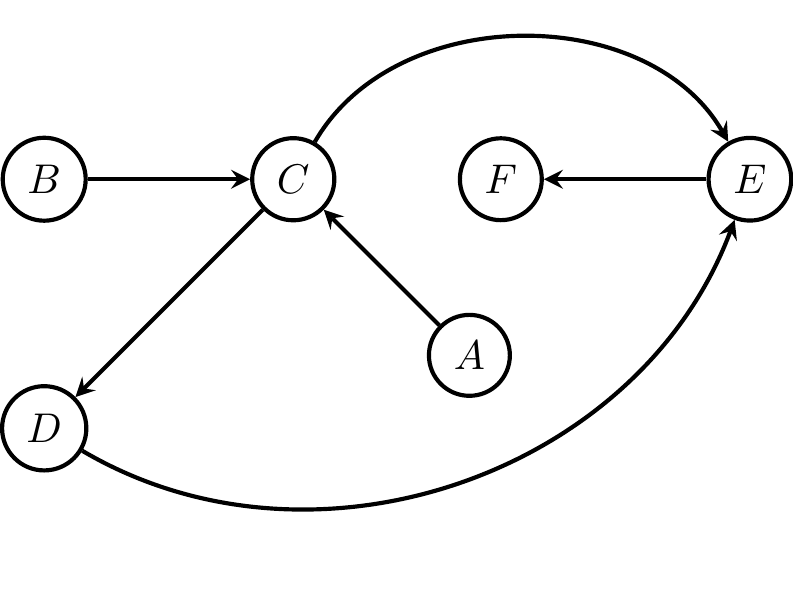
Exercise 5.12

Give, in lexicographical order, all possible topological orderings of the following directed acyclic graph (DAG):

Exercise 5.13

If we added an isolated vertex to the previous graph, how many topological orderings would it have? (Do not write them out, just say how many and explain why).

Exercise 5.14

An inverse topological ordering of a DAG is a sequence formed by all the vertices of the graph in such a way that if (v, w) is an edge of the graph, then w appears before v in the sequence.

Starting from the algorithm for depth-first traversal, design and analyse an algorithm that obtains an inverse topological ordering of a DAG.