Squaring

Exercises 5.17 and 5.18

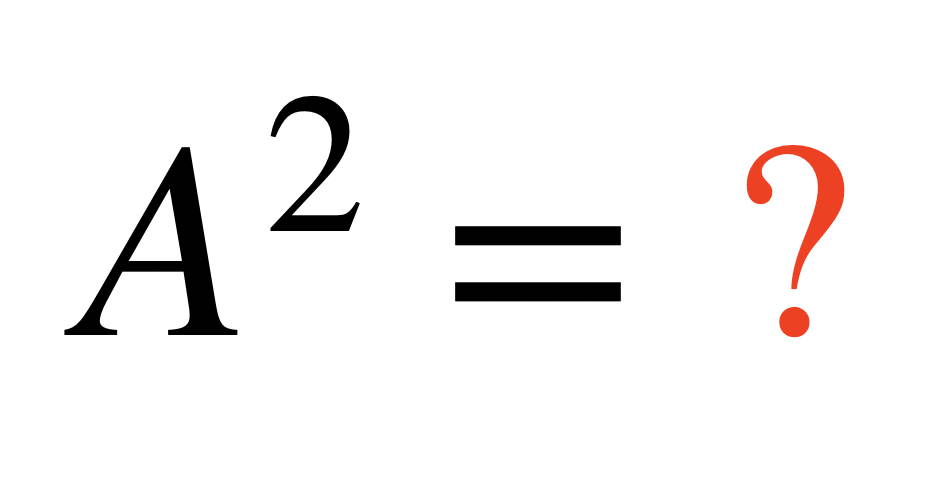
Exercise 5.17

The square of a graph G = (V, E) is another graph G^s = (V, E^s) where E^s =\{\{u,v\} : \exists w\in V\ \{u,w\}\in E\wedge \{w,v\}\in E\}.

Design and analyze an algorithm that, given a graph G represented as an adjacency matrix, calculates the adjacency matrix of G^s.

Design and analyze an algorithm that, given a graph G represented as adjacency lists, calculates the adjacency lists of G^s.

Exercise 5.18

Can the square of an n-vertex graph represented with an adjacency matrix be calculated in time lower than \Theta(n^3)?

Hint

Strassen.