EDA T4 — Divide and Conquer

Ilario Bonacina

ilario.bonacina+EDA@upc.edu

This presentation is an adaptation of material from Antoni Lozano and Conrado Martinez

Agenda

Last theory class

Divide-and Conquer paradigm
- Master Theorem for divide-and-conquer recurrences (revision)
- Binary Search (revision)
- Mergesort
- Quicksort

Today

Mathematical algorithms
- Fast exponentiation (revision)
- Integer multiplication
- Matrix multiplication
Selection
- Quickselect

Before we start: Questions?

Exponentiation

Input:

numbers x\in \mathbb Q and n\in \mathbb N

Goal:

output x^n

Why?

Biology
- Population Growth and Decay
Finance and Economics
- Compound Interests
Cryptography
- RSA public-key cryptosystem

Fast exponentiation

double power(double x, int n) {
    if (n == 0) {
        return 1;
    } 
    else {
        double y = power(x, n/2);
        if (n % 2 == 0) 
            return y * y;
        else 
            return y * y * x;
    } 
}

This exponentiation algorithm is based on the following algebraic identities: \begin{cases} x^0 &= 1\\ x^{2n}&=x^n\cdot x^n\\ x^{2n+1}&=x^{n}\cdot x^n\cdot x \end{cases}

Let C(n) be the cost of the algorithm as a function of the exponent size n. The recursion for C(n) is C(n)=C(n/2)+\Theta(1). Which gives C(n) =\Theta(\log n)\ .

Code it!

Jutge exercises on Fast Exponentiation.

P29212 Modular exponentiation (similar to Problem 1.23 from problem class P2)
P61833 Powers of a matrix
P74219 Fibonacci numbers (2)

Why Fibonacci is in this block of exercises?
If you don’t remember why, revise the slides from class T2.
X39049 Powers of permutations

Integer multiplication

Input:

two n-bits numbers x,y\in \mathbb N

Goal:

compute x\cdot y

Why?

integer multiplication is used almost everywhere

Naïve/Grade-school/Standard multiplication algorithm

Cost of the naïve multiplication algorithm: \Theta(n^2)

Also the Russian peasant/Ancient Egyptian multiplication algorithm has cost \Theta(n^2).

A divide-and-conquer strategy

Let x and y be two as n-digits numbers in base 2. Assume for simplicity n=2^k for some k.¹

Let x=x_1 2^{n/2}+x_2 and y=y_1 2^{n/2}+y_2.

\begin{align*} xy &=(x_1 2^{n/2}+x_2)(y_1 2^{n/2}+y_2)\\ & =x_1 y_1 2^{n} + (x_1y_2+x_2y_1)2^{n/2}+ x_2 y_2 \end{align*}

A divide-and-conquer strategy to compute xy:

we compute the 4 products x_1y_1, x_1y_2, x_2y_1, x_2y_2, and then
combine these intermediate results using sums and shifts.

The cost of the sums and the shifts is \Theta(n). Hence, the cost M(n) of this divide-and-conquer multiplication algorithm satisfies the recurrence

M(n) = 4·M(n/2) + \Theta(n)

By the Master Theorem (check!) this gives M(n)=\Theta(n^2).

Is integer multiplication always \Omega(n^2)?

In 1960 Andrey Kolmogorov started a seminar at Moscow State University on the complexity of computation where he stated the conjecture that any algorithm for integer multiplication of n-bits numbers would require \Omega (n^{2}) elementary operations.

Within a week Anatoly Karatsuba (at the time 23 years old) disproved the conjecture!

Karatsuba showed how to multiply to n-bits integer numbers using \Theta(n^{\log_2 3})=\Theta(n^{1.58...}) elementary operations.

Karatsuba’s algorithm

\begin{align*} xy &=(x_1 2^{n/2}+x_2)(y_1 2^{n/2}+y_2)\\ & =x_1 y_1 2^{n} + (\textcolor{blue}{x_1y_2+x_2y_1})2^{n/2}+ x_2 y_2 \\ &=x_1 y_1 2^{n} + (\textcolor{blue}{(x_1+x_2)(y_1+y_2)-x_1 y_1-x_2 y_2})2^{n/2}+ x_2y_2 \end{align*}

Karatsuba’s divide-and-conquer strategy to compute xy:

compute x_1+x_2 and y_1+y_2
compute the 3 products x_1y_1, x_2y_2 and (x_1+x_2)(y_1+y_2), and then
combine these intermediate results using sums/subtractions and shifts.

The cost of the sums and the shifts is \Theta(n). Hence, the cost K(n) of this divide-and-conquer multiplication algorithm satisfies the recurrence

K(n) = 3·K(n/2) + \Theta(n)

By the Master Theorem (check!) this gives K(n)=\Theta(n^{\log_2 3}).

The world post-Karatsuba…

Cost	Year	Who	Details
\Theta(n^2)	\sim 1700 BC	Some anonymous babylonian/egyptian	Still good for n \leq \sim 10^{96}
\Theta(n^{\log_2 3})=\Theta(n^{1.5849...})	1960	Karatsuba	Faster than naïve multiplication after n \geq \sim 10^{96}
\Theta(n \log n \cdot 2^{\sqrt{n\log n}})	1963-2005	Toom-Cook-Knuth	Generalization of Karatsuba splitting into more than 2 parts
\Theta(n\log n \cdot \log\log n)	1971	Schönhage-Strassen	Uses the Fast Fourier Transform. Outperforms Toom-Cook-Knuth for n \geq \sim 10^{10^4}
\mathcal O(n\log n \cdot 2^{\Theta(\log^* n)})	2007	Fürer	Outperforms Schönhage-Strassen for n\geq \sim 10^{10^{18}}. (\ \log^*(n) is the number of times the logarithm function must be iteratively applied before the result is \leq 1.)
\Theta(n\log n \cdot 2^{3\log^* n})	2015	Harvey et al	Similar to Fürer’s algorithm.
\Theta(n\log n)	2019	Harvey & van der Hoeven	Is \Theta(n\log n) the best we can do for integer multiplication? We don’t know! The best lower-bound known is the trivial one: \Omega(n)!!

In practice

Toom-Cook and Karatsuba: are used for intermediate-sized numbers, basically until Schönhage-Strassen is used. We use them every day when we do e-banking or when we use GitHub involving RSA keys, since RSA numbers are hundreds or thousands of digits long.

Schönhage-Strassen algorithm: is used in GNU multi-precision library for numbers with 33.000 to 150.000 digits. It is used mainly in number theory for things like calculating record numbers of digits in \pi, and for practical applications such as multiplying polynomials with huge coefficients.

Harvey & van der Hoeven 2019 \Theta(n\log n) algorithm: is a galactic algorithm. It does not have real-world applications.

Matrix multiplication

Input:

two n\times n matrices A,B with rational entries

Goal:

compute A\cdot B

Why?

Graphics — scalings, translations, rotations, etc
- 3D rendering applications
Graph theory
- counting walks between nodes in a graph
Linear discrete dynamical systems
Deep learning and convolutional neural networks
Quantum computing
…

Naïve matrix multiplication algorithm – revision

// Naïve Matrix Multiplication
typedef vector<double> Row;
typedef vector<Row> Matrix;
// we define a multiplication operator that
// can be used like this: Matrix C = A * B;
// Pre: A[0].size() == B.size()
Matrix operator*(const Matrix& A, const Matrix& B) {
    if (A[0].size() != B.size()) 
        throw IncompatibleMatrixProduct;
    int m = A.size();
    int n = A[0].size();
    int p = B[0].size();
    Matrix C(m, Row(p, 0.0)); 
    // C = m x p matrix initialized to 0.0
    for (int i = 0; i < m; ++i)
        for (int j = 0; j < p; ++j)
            for (int k = 0; k < n; ++k)
                C[i][j] += A[i][k] * B[k][j];
    return C;
}

The algorithm on the left computes the matrix C=(C_{ij})_{m\times p} product of A=(A_{ij})_{m\times n} and B=(B_{ij})_{n\times p} using the definition:

\displaystyle C_{ij} = \sum_{k=0}^{n}A_{ik}B_{kj}\ .

For square matrices, where n=m=p, the cost is \Theta(n^3).

A divide-and-conquer approach

Given two square matrices A,B, say for simplicity of dimension n\times n when n is a power of 2.¹ Let’s partition A and B into equal size sub matrices A=\begin{pmatrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{pmatrix} \quad B=\begin{pmatrix}B_{11}&B_{12}\\B_{21}&B_{22}\end{pmatrix}

\begin{pmatrix} A_{11} & A_{12}\\ A_{21} & A_{22} \end{pmatrix} \cdot \begin{pmatrix} B_{11} & B_{12}\\ B_{21} & B_{22} \end{pmatrix} = \begin{pmatrix} A_{11}B_{11}+A_{12}B_{21} & A_{11}B_{12}+A_{12}B_{22}\\ A_{21}B_{11}+A_{22}B_{21} & A_{21}B_{12}+A_{22}B_{22} \end{pmatrix}

Now, the cost M(n) of multiplying two n\times n matrices would be the cost of computing 8 product of matrices \frac{n}{2}\times \frac{n}{2} (A_{11}B_{11}, etc) and doing 4 additions of \frac{n}{2}\times \frac{n}{2} matrices.

The addition has cost \Theta(\left(\frac{n}{2}\right)^2)=\Theta(n^2), hence the recurrence for M(n) is M(n)=8M(n/2)+\Theta(n^2)\ .

By the Master Theorem (check!) this gives M(n)=\Theta(n^3).

Is matrix multiplication always \Omega(n^3)?

Let’s try to address a simpler problem. How many multiplications do we need to compute the product of two 2 by 2 matrices?

The definition gives 8 multiplications, but can we do better (perhaps using more additions/subtractions)?

Yep! We can use 7 multiplications! (Strassen 1969) 🤯

Winograd, 1971: 7 multiplications are also needed to compute the product of 2\times 2 matrices

Multiply 2 by 2 matrices with 7 multiplications

\begin{aligned} M_{1}&=(A_{11}+A_{22}){\color {red}\cdot }(B_{11}+B_{22}); \\ M_{2}&=(A_{21}+A_{22}){\color {red}\cdot }B_{11}; \\ M_{3}&=A_{11}{\color {red}\cdot }(B_{12}-B_{22}); \\ M_{4}&=A_{22}{\color {red}\cdot }(B_{21}-B_{11}); \\ M_{5}&=(A_{11}+A_{12}){\color {red}\cdot }B_{22}; \\ M_{6}&=(A_{21}-A_{11}){\color {red}\cdot }(B_{11}+B_{12}); \\ M_{7}&=(A_{12}-A_{22}){\color {red}\cdot }(B_{21}+B_{22}) \end{aligned}

\begin{pmatrix} A_{11} & A_{12}\\ A_{21} & A_{22} \end{pmatrix} \!\cdot\! \begin{pmatrix} B_{11} & B_{12}\\ B_{21} & B_{22} \end{pmatrix} = \begin{pmatrix} M_{1}+M_{4}-M_{5}+M_{7} & M_{3}+M_{5}\\ M_{2}+M_{4} & M_{1}-M_{2}+M_{3}+M_{6} \end{pmatrix}

Wait what? How could someone come-up with this?? 🤯

A possible way…

There are several articles/books giving possible explanations of how one could come-up with Strassen’s 7 multiplication algorithm (or to something equivalent). I’ll try to do this adaptating of A simple proof of Strassen’s result by Gideon Yuval and the cs.stackexchange post by Yuval Filmus.

The core of Strassen’s algorithm is to show how to compute \begin{pmatrix} a &b \\ c & d \end{pmatrix} \cdot \begin{pmatrix} e & f\\ g & h \end{pmatrix} \tag{1} using 7 multiplications instead of 8 as the definition of matrix product would give.

This problem is equivalent to computing the entries of the vector given by

\begin{pmatrix} a & 0 & b & 0\\ 0 & a & 0 & b \\ c & 0 & d & 0\\ 0 & c & 0 & d \end{pmatrix} \cdot \begin{pmatrix} e \\ f \\ g \\ h \end{pmatrix}

Let M=\begin{pmatrix} a & 0 & b & 0\\ 0 & a & 0 & b \\ c & 0 & d & 0\\ 0 & c & 0 & d \end{pmatrix}, to prove Equation 1 it is enough to show that

M=\ell_1M_1+\ell_2 M_2+ \ell_3 M_3 +\ell_4 M_4+\ell_5 M_5 +\ell_6 M_6 +\ell_7 M_7 \tag{2} where each \ell_i is a linear combination of a,b,c,d and each M_i is a rank 1 matrix. Since each M_i is rank 1 this means there exist vectors x_i,y_i such that M_i=x_iy_i^T.

Before showing how to construct the M_is let’s see first how a decomposition as the one in Equation 2 implies that Equation 1 can be computed using 7 multiplications:

\begin{align*} M\cdot \begin{pmatrix} e \\ f \\ g \\ h \end{pmatrix} & = \sum_{i=1}^ 7 \ell_i M_i\cdot \begin{pmatrix} e \\ f \\ g \\ h \end{pmatrix} \\ & = \sum_{i=1}^7\ell_i x_iy_i^T\cdot \begin{pmatrix} e \\ f \\ g \\ h \end{pmatrix} \\ & = \sum_{i=1}^7\ell_i r_i x_i\ , \end{align*} where r_i=y_i^T\cdot \begin{pmatrix} e \\ f \\ g \\ h \end{pmatrix}, that is r_i is a linear combination of e,f,g,h. This shows that each entry of Equation 1 is some linear combination of the products \ell_i r_i.

To conclude it is enough then to come up with a decomposition of M of the form given in Equation 2.

We could start by cancelling the top left and bottom right entries, in a way which avoids hitting zero entries: \begin{pmatrix} a & 0 & b & 0\\ 0 & a & 0 & b \\ c & 0 & d & 0\\ 0 & c & 0 & d \end{pmatrix} = \begin{pmatrix} a & 0 & a & 0\\ 0 & 0 & 0 & 0 \\ a & 0 & a & 0\\ 0 & 0 & 0 & 0 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 & 0\\ 0 & d & 0 & d \\ 0 & 0 & 0 & 0\\ 0 & d & 0 & d \end{pmatrix} + \begin{pmatrix} 0 & 0 & b -a & 0\\ 0 & a -d & 0 & b -d \\ c -a & 0 & d-a & 0\\ 0 & c -d & 0 & 0 \end{pmatrix} The first two matrices are rank 1, so to conclude we need to show how to decompose the matrix \begin{pmatrix} 0 & 0 & b -a & 0\\ 0 & a -d & 0 & b -d \\ c -a & 0 & d-a & 0\\ 0 & c -d & 0 & 0 \end{pmatrix} as a sum of 5 matrices of rank 1. This matrix is a bit messy. We could try to fix this by “flipping” the inner square:

\begin{pmatrix} 0 & 0 & b -a & 0\\ 0 & a -d & 0 & b -d \\ c -a & 0 & d-a & 0\\ 0 & c -d & 0 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & 0\\ 0 & a -d & a- d & 0 \\ 0 & d-a & d-a & 0\\ 0 & 0 & 0 & 0 \end{pmatrix} + \begin{pmatrix} 0 & 0 & b -a & 0\\ 0 & 0 & d-a & b -d \\ c -a & a-d & 0 & 0\\ 0 & c -d & 0 & 0 \end{pmatrix}

The first matrix is rank 1, so to conclude we need to decompose \begin{pmatrix} 0 & 0 & b -a & 0\\ 0 & 0 & d-a & b -d \\ c -a & a-d & 0 & 0\\ 0 & c -d & 0 & 0 \end{pmatrix} as a linear combination of 4 rank 1 matrices. This can be done as follows:

\begin{align*} \begin{pmatrix} 0 & 0 & b -a & 0\\ 0 & 0 & d-a & b -d \\ c -a & a-d & 0 & 0\\ 0 & c -d & 0 & 0 \end{pmatrix} & = \begin{pmatrix} 0 & 0 & b -a & 0\\ 0 & 0 & b -a & 0 \\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 & 0\\ 0 & 0 & d-b & b -d \\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix} \\ &+ \begin{pmatrix} 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \\ 0 & c-d & 0 & 0\\ 0 & c -d & 0 & 0 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \\ c -a & a-c & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix} \end{align*}

Strassen’s algorithm for matrix multiplication

Now, using Strassen decomposition the cost S(n) of multiplying two n\times n matrices would be the cost of computing 7 product of matrices \frac{n}{2}\times \frac{n}{2} and doing 18 additions of \frac{n}{2}\times \frac{n}{2} matrices.

The addition has cost \Theta(\left(\frac{n}{2}\right)^2)=\Theta(n^2), hence the recurrence for S(n) is S(n)=7S(n/2)+\Theta(n^2)\ .

By the Master Theorem (check!) this gives S(n)=\Theta(n^{\log_2(7)})=\Theta(n^{2.807...})\ .

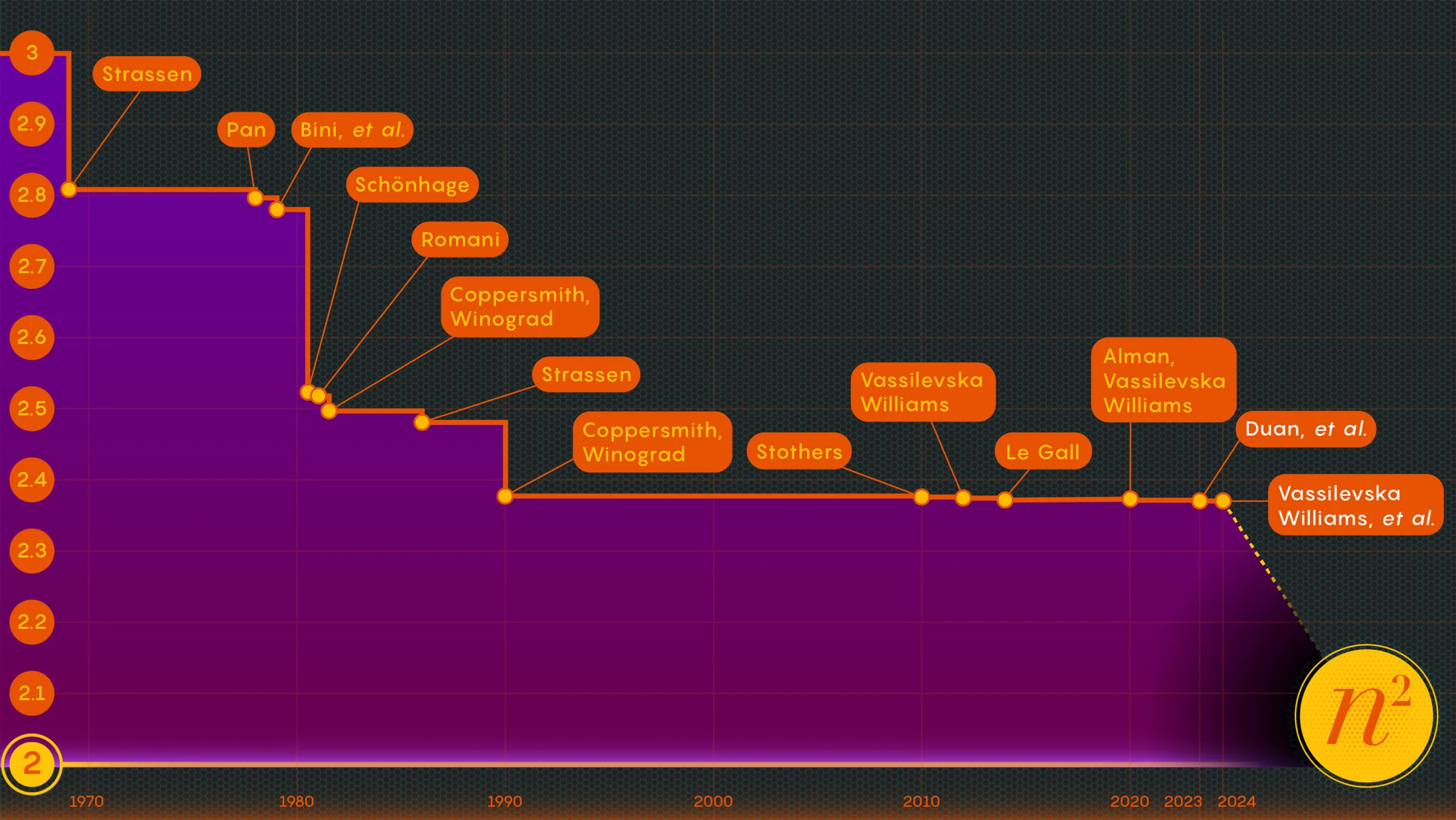
The world post-Strassen…

Is matrix multiplication always \Omega(n^3)? No!!

In practice

Strassen’s \Theta(n^{\log_2(7)}) algorithm is faster in practice than the naïve matrix multiplication algorithm, only for n\geq \sim 500: the hidden constants and lower order terms in the cost are quite big and their impact in the cost cannot be disregarded except when n is large enough.

Selection

Input:

an array A[1..n]
an integer j between 1 and n

Goal:

output the jth smallest element of A

Finding the median of A is a special case of the problem above when j=\lfloor (n+1)/2\rfloor.

Finding the max and min of A are also special cases.

Upper and lower bounds

We can solve the Selection problem in cost \Theta(n\log n), where n is the number of elements in the input array. How?
To solve the selection problem we need at least to look at all the input, i.e. we need cost at least \Omega(n).
We can solve the selection problem when j=1 or j=n in cost \Theta(n) (How?).

Wait: can we always solve the selection problem in cost \Theta(n)?

Yes!

QuickSelect — the cousin of quicksort

QuickSelect (Hoare, 1962), also known as Find and as one-sided Quicksort, is a variant of Quicksort adapted to select the j-th smallest element in an n-elements array.

// Quicksort
template <typename T>

void quicksort(vector<T>& A) {
    quicksort(A, 0, A.size() - 1);
}

void quicksort(vector<T>& A, int left, int right) {
    if (left < right) {
        int q = partition(A, left, right);
        quicksort(A, left, q - 1);
        quicksort(A, q + 1, right);
    } 
}

1: The pivot ends up in position q of the array.

Once the partition finishes, suppose that the pivot ends at position q. Then A[left..q−1] contains the elements that will end up in position 1 up to q-1 and A[q+ 1..right] contains the elements that will end up in positions q+1 to right.

QuickSelect

// Quickselect
// ASSUMPTION: ALL ELEMENTS IN A[] ARE DISTINCT.
int quickselect(vector<int>& A, int left, int right, int j) {
    if (j > 0 && j <= right - left + 1) {
        // Partition the array as in quicksort
        int q = partition(A, left, right);
        if (q - left == j - 1)
            return A[q];
        if (q - left > j - 1) 
            return quickselect(A, left, q - 1, j);
        return quickselect(A, q + 1, right, j - q + left - 1);
    }
    return -1;
}

If j=1+q - left we are done: we have found the element.
If j<1+q - left then we recursively continue in the left subarray A[left..q−1]
If j>1+q - left then the element must be located in the right subarray A[q+1..right]. Be careful that now we are not looking for the jth element anymore!

It is possible to prove that the worst case of quickselect is \Theta(n^2).
While the average case (assuming the uniform distribution) is \Theta(n).

Can we modify the algorithm above to get worst case \Theta(n)? Yes!

Worst-case linear time selection

In 1973 Blum, Floyd, Pratt, Rivest and Tarjan designed a selection algorithm with linear worst-case cost. They do this modifying Hoare’s QuickSelect. The goal is

to guarantee that the pivot that we choose in each recursive step will divide the array into two subarrays such that their respective sizes are a fraction of the original size n.
to pick such a pivot with cost \mathcal O(n).

The idea is to use quickselect recursively to choose the pivot too!

Median of medians

The algorithm will pick as pivot the so-called median of medians (or also called pseudo-median). This is computed as follows:

choose an odd constant k …We will choose this later!
divide the input array A into \lceil n/k\rceil blocks of k elements each. Except possibly the last block that might contain less than k elements.
compute the medians of all the blocks.
call quickselect to find the median of all the \lceil n/k\rceil medians calculated: this is the median of medians.

Median of medians as the pivot

The median-of-medians m has the property that the number of elements smaller than m in the input array is least \frac{n}{2k}\cdot\frac{k}{2}=\frac{n}{4} (why?).¹

That is, if we choose as pivot the median-of-medians, we partition the input array into two parts of size at most \frac{3n}{4} elements.

Let’s find a recurrence for the cost S(n) of quickselect on an array of n elements.

Median-of-medians — the worst-case cost

The algorithm will pick as pivot the so-called median of medians (or also called pseudo-median):

choose an odd constant k …We will choose this later!
divide the input array A into \lceil n/k\rceil blocks of k elements each. Except possibly the last block that might contain less than k elements.
compute the medians of all the blocks.
The cost of computing each median is \Theta(1) (why?), but there are \lceil n/k\rceil-many of them, so the total cost of this step is \Theta(n)
call quickselect to find the median of all the \lceil n/k\rceil medians calculated: this is the median of medians.
This has cost S(n/k)

QuickSelect with median-of-medians pivot – worst-case cost

Putting everything together, the worst-case cost of the QuickSelect with median-of-medians pivot satisfies the recurency

S(n) \leq \Theta(n) + S(n/k) + S(3n/4)

It is possible to prove (for instance by induction or inspecting the recursion tree) that if we choose k such that \frac{3}{4}+\frac{1}{k}<1 then S(n)=\mathcal O(n).

k=5 works.

Since clearly S(n)=\Omega(n), then S(n)=\Theta(n).

Upcoming classes

Wednesday: Problem class P3 on divide-and-conquer algorithms (do the exercises before class).
Next Monday: Theory class T5 on Dictionaries!

Questions?