EDA T5 — Dictionaries

Ilario Bonacina

ilario.bonacina+EDA@upc.edu

This presentation is an adaptation of material from Antoni Lozano and Conrado Martinez

Agenda

Last theory class

Mathematical algorithms
- Fast exponentiation (revision)
- Integer multiplication
- Matrix multiplication
Selection
- Quickselect

Today

Dictionaries
- Hash Tables
- Binary Search Trees

Before we start: Questions on previous material?

Dictionaries

Dictionary

A dictionary (or map in the STL of C++) is a data structure that stores a finite set of elements, each one associated to a unique identifier or key, and that supports search by key and (usually) insertions/deletions.

Example 1 A dictionary could store information about the students at the UPC using as key the DNI numbers associated to each student.

Would it be a good alternative to use as key the full name?

No. Although unlikely, two students might have exactly the same full name.

Example 2 A dictionary could be the set of accounts in a bank. The keys are the account numbers while the information is the owner, the type of account, the balance, the movements on the account, …

Typical operations

search: given a key find the element of the dictionary with that key (if present)
insertion: adding an element (key,info) to the dictionary
deletion: given a key, delete the element with that key (if present)
size: returns the number of elements in the dictionary

Dictionary

We can think of dictionaries as functions f\colon K \to I\ , with domain a set of keys K and range a set of information/values I.

f(k)=i, means that the information/value i is associated to the key k.

template <typename Key, typename Value>

class Dictionary {
    public:
        Dictionary();
        ~Dictionary();
        ...
        void lookup(const Key& k, bool& exists, Value& v) const;
        void insert(const Key& k, const Value& v);
        void remove(const Key& k);
        ...
    private:
    ...
}

Example: sets

Example 3 (Finite sets as dictionaries) We can see a finite set S as a subset of a possibly larger set of keys K, and the information associated to each key is a Boolean value, indicating whether the given key is in S or not. In other words, the function f is the indicator function of S.

If S \subseteq K=\{0,\dots,m−1\} for some relatively small value m (the number of elements in the set is not \ll m or m is not too large), we can implement a dictionary on S as a bitvector.

Search (= membership), insertions and deletions can be done in \Theta(1) time. Bitvectors also efficiently support unions (bit-wise OR), intersections (bit-wise AND), etc.

Sorted dictionaries

A subfamily of dictionaries of particular interest are those called sorted, supporting sequential traversal of the elements in increasing order of their keys.¹ The dictionary class then provides methods to iterate through all the elements in the dictionary in ascending order of their keys.

In C++ dictionary classes, this is usually done with iterators.

Example 4

Prints the chemical elements in alphabetic order together with their atomic weight

Dictionary<string, double> PeriodicTable;
    ...
// an iterator it into a Dictionary<Key,Value> points to a pair<Key,Value>

for (auto it : PeriodicTable) {
    cout << it->first << ": " << it->second << endl;
}

Additional operations

Usually dictionary classes supports additional operations:¹

Set-theoretic operations: unions, intersections, set difference, …

Search and removal by rank: find/remove the element with the i-th smallest key, …

Search and removal in ranges: given the keys k_1 and k_2, find/remove all elements which key k is s.t. k_1\leq k\leq k_2

Counting: count how many elements have a key less/greater than a given key k, …

A first implementation: linked-lists

An unsorted linked list can be used to implement a dictionary, with each element of the list storing a pair ⟨key,value⟩. The cost of searches, insertions and deletions is \Theta(n), where n is the size of the dictionary.

This can be acceptable if n is small, e.g., n\leq 250.

Warning

Unsorted linked lists should not be used to implement a dictionary if we need to access the dictionary in sorted order.

Other implementations

hash tables (today!)
binary search trees (today!)
AVL trees (next class!)
Skip lists (in some other course)
Tries (in some other course)
…

Hash Tables

Hash tables

Hash tables (cat: taules de dispersió, esp: tables de dispersión) are efficient data structures to store dictionaries. They were introduced in 1954 by W. W. Peterson and can be seen as generalizations of vectors.

The worst case cost of search/insertion/deletion could be \Theta(n) but (under reasonable assumptions) the expected cost is \Theta(1).

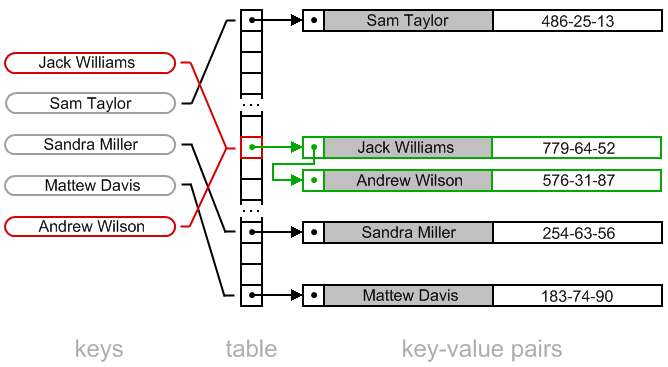
Instead of storing all the elements in a single linked list, first create M buckets. Then use a function h to associate each key in K with one bucket.

We want the function h to spread the keys as evenly as possible among the buckets, i.e. ideally we would like to have about \frac{|K|}{M} elements in each bucket.

Then we could store all the keys mapped to the same bucket (the so called collisions) as a linked list. See this visually.

Hash functions

A hash function h maps the set of n keys K into \{0,1,2,\dots,M-1\}, the set of indices or addresses of the table.

A good hash function

must be deterministic (why?)
should be easy to compute
should spread evenly the keys, for each 0\leq i< M, |\{k\in K \colon h(k)=i \}|\approx \frac{|K|}{M}=\frac{n}{M}

Example 5 A dictionary could store information about the students at the UPC using as key the UPC ID number associated to each student.

Which is a better hash function: taking the first digit of the UPC ID number or the last digit?

Defining a good hash function is not an easy task!

This task is very closely related to the definition of good (pseudo)random number generators.

As a general rule, the keys (if they are not already natural numbers) are first converted to natural numbers (reading the binary representation of the key as a number), then some mathematical transformation is applied, taking the result modulo m (the size of the table).

For various theoretical reasons, it is a good idea that m is a prime number.

Within #include <utility> there is already defined a good hash function.

Collision resolution

Collision resolution strategies can be grouped into two main families

Open hashing

separate chaining (the one we saw before). Each slot in the hash table has a pointer to a linked list of synonyms (keys that the hash function maps to the same value).
coalesced hashing
…

Open addressing

linear probing
double hashing
quadratic hashing
…

Hash table separate chaining — implementation

#include <utility>
#include <list>
#include <vector>
using namespace std;
template <typename Key, typename Info>
class Dictionary {
    public:
        ...
        Info& query (const Key& key);
        void assign (const Key& key, const Info& info);
        void erase (const Key& key);
        ....
    private:
        typedef pair<Key, Info> Pair;
        typedef list<Pair> List;
        typedef typename List::iterator iter;
        vector<List> t; // Hash table
        int n; // Number of keys
        int M; // Number of positions
        ...
};

See the full implementation in the Algorismes en C++.

Search in Separate chaining

public:
    Info& query (const Key& key) {
        int h = hash(key) % M;
        iter p = find(key, t[h]);
        if (p != t[h].end()) return p->second;
        else throw "Key does not exist";
}
private:
    static iter find (const Key& key, list<Pair>& L) {
        iter p = L.begin();
        while (p != L.end() and p->first != key) ++p;
        return p;
    }

Returns a reference to the information associated to key. Throws a precondition exception if the key does not belong to the dictionary.
Worst-case cost: \Theta(n).
Average-case cost: \Theta(1 + n/M).

Insertion in Separate chaining

public: 
    void assign (const Key& key, const Info& info) {
        int h = hash(key) % M;
        iter p = find(key, t[h]);
        if (p != t[h].end()) p->second = info;
        else {
            t[h].push_back(Pair(key, info));
            ++n;
        } 
    }

Assigns info to key. If the key belongs to the dictionary already the associated information is modified.
Worst-case cost: \Theta(n).
Average-case cost: \Theta(1 + n/M).

Deletion in Separate chaining

public:
    void erase (const Key& key) {
        int h = hash(key) % M;
        iter p = find(key, t[h]);
        if (p != t[h].end()) {
            t[h].erase(p);
            --n;
        } 
    }

Erases key and its associated information from the dictionary. If the key does not belong to the dictionary, nothing changes.
Worst-case cost: \Theta(n).
Average-case cost: \Theta(1 + n/M).

The average cost of separate chaining

Let n be the number of elements stored in the hash table. On average, each linked list contains \alpha= n/M elements. The value \alpha is called load factor, and the performance of the hash table will be dependent on it.

The average cost of lookups (either successful or unsuccessful), of insertions and of deletions will be proportional to the load factor \alpha=\frac{n}{M}. If \alpha is a small constant value then the cost of all basic operations is, on average, \Theta(1). However, it can be shown that the expected length of the largest synonym list is \Theta(\log n).

Graphs interlude: Trees

Trees

What is a tree?

In Computer Science a tree is a connected acyclic graph.

Trees

In Computer Science a tree is a connected acyclic graph.

Graph
Connected graph
Cycles and acyclic Graph

A graph G is a pair of sets G=(V,E) where V is a finite set (the vertices of the graph), and E is a set of un-ordered pairs of distinct vertices (the edges).

Graphs can be visualized with drawings where vertices are cicles and edges lines between circles. For example

A graph G=(V,E) is connected if for every two vertices u,w\in V there is a sequence of vertices v_1,v_2,\dots, v_k where v_1=u, v_k=w and for every i, \{v_i,v_{i+1}\}\in E. A sequence of vertices/edges of this form is a walk from u to w. It is a trail if all edges are distinct. If also all vertices are distinct it is a path.

A cycle in a graph is a trail where the first and last vertices are equal. A graph is acyclic if there are no cycles in it.

Which of the following are connected, acyclic, trees?

\emptyset

Rooted trees

A rooted tree is a tree with a distinguished vertex (the root). The root is usually put on top.

Further tree terminology

leaf: any vertex with only one edge to it

internal node: any vertex which is not a leaf

depth/height: the largest distance (number of edges in a trail) from the root to a leaf

parent/child/siblings: in an edge \{x,y\}, the vertex closest to the root is the parent and the other is the child. Vertices with the same parent are siblings

predecessor/successor: all the nodes in the trail from the root to x are the predecessors of x. If y is predecessor of x, then x is a successor of y.

Binary Trees

A (rooted) tree where each vertex has \leq 2 children is a binary tree. They are usually called the left and right child. The tree with root the left (resp. right) child and having as vertices only the successors of it is called left subtree (resp. right subtree).

Height of binary trees

If a binary tree has n vertices its height h satisfies:

\lfloor\log_2(n)\rfloor \leq h \leq n - 1

An example of a binary tree where h= n-1?

An example of a binary tree where h= \lfloor\log_2(n)\rfloor?

We will use binary trees in two ways:

to implement dictionaries
- Binary Search Trees
- AVL trees (next class)
to implement priority queues
- Heaps (next class)

Binary Search Trees

A Binary Search tree (cat: Arbre Binari de Cerca, ABC) is a binary tree such that each vertex v in it has associated a key \mathsf{KEY}(v) and

for each vertex w in the left subtree of v, \mathsf{KEY}(w)<\mathsf{KEY}(v),
for each vertex u in the right subtree of v, \mathsf{KEY}(u)>\mathsf{KEY}(v).

Which of the following is a BST?

Implementation¹

template <typename Key, typename Info>
class Dictionary {
    public:
        Info& query (const Key& key);
        void assign (const Key& key, const Info& info);
        void erase (const Key& key);
        ...
    private:
        struct Node {
            Key key;
            Info info;
            Node* left; // Pointer to left child
            Node* right; // Pointer to right child
            Node (const Key& k, const Info& i, Node* l, Node* r)
            : key(k), info(i), left(l), right(r) { }
        };
        int n; // Number of keys
        Node* root; // Pointer to the root of the BST
};

Search in a BST

Let T be a BST representing the dictionary and let k be the key we are looking for.

If the BST T is empty then k is not in the dictionary. We need only to signal this event in some convenient way (e.g. returning false).
If T is not empty, let r its root. We have three possibilities:
- k=\mathsf{KEY}(r): the search is successful and we can stop it, returning r or the information associated to r which we care about
- k<\mathsf{KEY}(r): make a recursive call on the left subtree of r
- k>\mathsf{KEY}(r): make a recursive call on the right subtree of r

Search in a BST — implementation

public:
    Info& query (const Key& key) {
        if (Node* p = find(root, key)) return p->info; 
        else throw "Key does not exist";
    }
private:
    static Node* find (Node* p, const Key& key) {
        if (p) {
            if (key < p->key) return find(p->left, key);
            else if (key > p->key) return find(p->right, key);
        }   
        return p;
    }

query Returns a reference to the information associated to key. Throws a precondition exception if the key does not belong to the dictionary.
Worst-case cost: \Theta(h).

find Returns a pointer to the node of the tree pointed by p that contains key, or nullptr if the key is not there.
Worst-case cost: \Theta(t) where t is the height of the tree pointed by p.

Insertion in a BST — implementation

We can do insertions by the same reasoning as for the search: if the new key to be inserted is smaller than the key at the root insert in the left subtree; otherwise, insert into the right subtree. Each insertion will always create a new leaf.

public:
    void assign (const Key& key, const Info& info) {
        assign(root, key, info);
    }
private:
    void assign (Node*& p, const Key& key, const Info& info) {
        if (p) {
            if (key < p->key) assign(p->left, key, info);
            else if (key > p->key) assign(p->right, key, info);
            else p->info = info;
        } 
        else {
            ++n;
            p = new Node(key, info, nullptr, nullptr);
        } 
    }

Worst case cost of the public assign \Theta(h).

See the algorithm in action here.

Deletion in a BST

Deleting an element with given key k involves two phases:

Locating the node with key k(if any) in the tree
Removing that node

The first phase is a search. For the second phase,

if the node is a leaf (both subtrees are empty) then it suffices to remove the node.
When the node x to be removed has only one non-empty subtree, it is not very difficult to remove the node: lift the non-empty subtree so that the father of x points to the subtree’s root instead of pointing to x.
When the node x has two non-empty subtrees… what do we do?

Deletion in BSTs (cont’d)

When the node x has two non-empty subtrees…

Option 1: find the minimum m of the right subtree of x and append as a left child of m the left subtree of x. This is not so good on the long run (why?)
Option 2: find the minimum m of the right subtree of x swap-it with x and now remove x

See the algorithm in action here.

Finding the minimum in a BST

private:
    static Node* minimum (Node* p) {
        return p->left ? minimum(p->left) : p;
    }

    Node* extract_minimum (Node*& p) {
        if (p->left) return extract_minimum(p->left);
        else {
            Node* q = p;
            p = p->right;
            return q;
        } 
    }

minimum return a pointer to the node that contains the minimum element in the subtree pointed by p. extract_minimum extracts the node that contains the minimum element from the tree pointed by p. Returns a pointer to it.
Worst-case cost of both: \Theta(t) where t is the height of the tree pointed by p.

Deletion in a BST — implementation

public:
    void erase (const Key& key) {
        erase(root, key);
    }
private:
    void erase (Node*& p, const Key& key) {
        if (p) {
            if (key < p->key) erase(p->left, key);
            else if (key > p->key) erase(p->right, key);
            else {
                Node* q = p;
                if (!p->left) p = p->right;
                else if (!p->right) p = p->left;
                else {
                    Node* m = extract_minimum(p->right);
                    m->left = p->left; 
                    m->right = p->right;
                    p = m;
                    }
                delete q; 
                --n;
            } 
        } 
    }

Worst-case cost: \Theta(h).

Cost of Search/Insert/Delete in a BST — worst-case

For a BST of height h the worst-case cost of a search, an insertion or a deletion has cost \Theta(h). If the BST has n vertices its height h satisfies:

\lfloor \log_2(n)\rfloor \leq h \leq n-1

An example of BST where n insertions lead to a tree with height n-1?

In the worst-case, the height of BST of size n is \Theta(n), hence the worst-case cost of search, insertion and deletion is \Theta(n) too.

BSTs is that they can be very unbalanced. Can we keep them more balanced when doing insertions/deletions?

Yes! In next class we well see a very elegant solution, the AVL trees.

Cost of Search/Insert/Delete in a BST — average-case

In a BST tree built by n insertions, with all possible n! orderings of the n insertions being equally likely, on average, the height of a random BST is \Theta(\log n). Hence the cost of search/insert/delete is also \Theta(\log n).

Upcoming classes

Wednesday: Lab class L2 on divide-and-conquer algorithms (do the exercises before class).
Next Monday: Theory class T6 on Dictionaries and Priority Queues!

Questions?

EDA T5 — Dictionaries

Agenda

Last theory class

Today

Dictionaries

Dictionary

Typical operations

Dictionary

Example: sets

Sorted dictionaries

Additional operations

A first implementation: linked-lists

Other implementations

Hash Tables

Hash tables

Hash functions

Defining a good hash function is not an easy task!

Collision resolution

Hash table separate chaining — implementation

Search in Separate chaining

Insertion in Separate chaining

Deletion in Separate chaining

The average cost of separate chaining

Graphs interlude: Trees

Trees

Trees

Which of the following are connected, acyclic, trees?

Rooted trees

Further tree terminology

Binary Trees

Height of binary trees

Binary Search Trees

Binary Search Trees

Which of the following is a BST?

Implementation1

Search in a BST

Search in a BST — implementation

Insertion in a BST — implementation

Deletion in a BST

Deletion in BSTs (cont’d)

Finding the minimum in a BST

Deletion in a BST — implementation

Cost of Search/Insert/Delete in a BST — worst-case

Cost of Search/Insert/Delete in a BST — average-case

Upcoming classes

Implementation¹