Hashing and Hash Tables
A hash function h is a function that maps a large object \mathcal D (a genome, a string, a sequence of elements, etc.) into a smaller object (a shorter string, an integer in a small range, etc.). For simplicity, suppose h maps \mathcal D into the set of natural numbers \{0,1,\dots, M-1\}.
A hash function must be deterministic and easy to compute.
A hash function should try to produce different outputs for different inputs. This is not possible to happen for all inputs when M< |\mathcal D|, for instance. Actually, we should expect to find different elements mapping to the same number as soon as the number of elements in \mathcal D is \Omega(\sqrt M).
We say that two distinct elements x, y of \mathcal D collide (under the hash function h) if h(x) = h(y).
Ideally, a good hash function h should evenly distribute the elements of \mathcal D into \{0,1,\dots, M-1\}. That is, for every m\in M, \mathbb E[|\{x\in \mathcal D : h(x)=m\}|]\approx \frac{|\mathcal D|}{M}\ . In other words, on average we should expect about \frac{|\mathcal D|}{M}-many elements of \mathcal D being mapped to any particular value. The value \frac{|\mathcal D|}{M} is called the load factor and it is often denoted with the greek letter \alpha.
Defining a good hash function is not an easy task and it requires a solid background in several branches of Math. This task is very closely related to the definition of good pseudo-random number generators.
As a general rule, the keys are first converted to positive integers (reading the binary representation of the key as a number), some mathematical transformation is applied, taking the result modulo M. For various theoretical reasons, it is a good idea that M is a prime number.
Hash functions are extremely important, for instance in cryptography. Here we only see how to use hash functions to tell whether an element x is in \mathcal D or not efficiently.
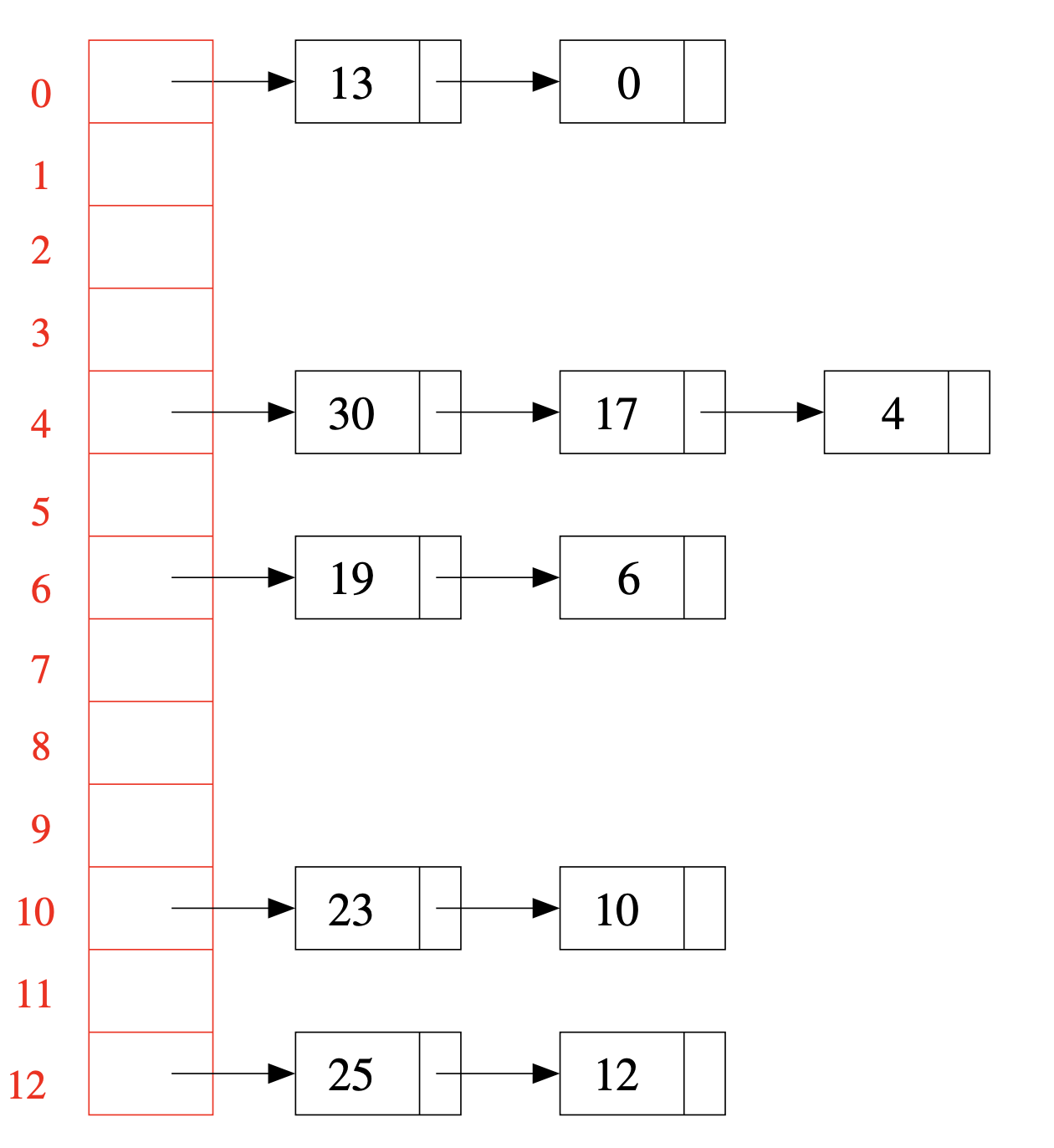
This is done using the so-called hash tables with separate chaining. First create M buckets. Then use a hash function h to associate each possible element in \mathcal D with one bucket. Then, to tell wether an element x is in \mathcal D or not we can just compute h(x), go to the bucket corresponding to h(x) and look the elements stored there one by one, until we find x or we have seen all elements of the bucket and we didn’t find x.
To achive this we can use an array A of linked lists, A[i] will correspond to the ith bucket. All the elements of \mathcal D mapped by h to i are stored in A[i] using a linked list.
Given \mathcal D=\{0, 4, 6, 10, 12, 13, 17, 19, 23, 25, 30\}, M=13 and h(x)= x\pmod M, then a hash table with separate chaining looks like the following.
Assuming a good hash function, i.e. one that spreads the elements approximately evenly, the expected time to look up for an element in a hash table is O(1 + \frac{|\mathcal D|}{M})=O(1+\alpha). So, if \alpha is a constant this is O(1).
For insertions in a hash table with separate chaining, we access the apropriate linked list using the hash function, and scan the list to find out whether the key was already present or not. If present, we modify the associated value; if not, a new node with the pair ⟨key,value⟩ is added to the list. Since the lists contain very few elements each, the simplest and more efficient solution is to add elements to the front.
There is no need for double links, sentinels, etc. Sorting the lists or using some other sophisticated data structure instead of linked lists does not report real practical benefits.