L3: Graph Algorithms I

In this lab we consider some of the problems from Jutge.org, section EDA \rightarrow Graph Algorithms. The problems in this section we see in this lab are of three different types

variations on Depth-First Search,
variations on Breath-First Search,
variations on Topological Sort.

Representation of graphs

The two most frequent ways to implement a graph are via adjacency matrices or adjacency lists. As a general rule, the preferred implementation will be adjancecy lists.

The graph G=(V,E) is represented using a matrix, called the adjacency matrix A with Boolean entries: the entry A[i][j] of the adjancency matrix A is a Boolean indicating whether (i,j) is an edge in E or not.

For weighted (directed) graph, the entry A[i][j] stores the label/weight assigned to the edge (i,j).

Pro: we can answer very efficiently whether an edge (u,v) \in E or not. Moreover, linear algebra calculations on A reveal properties of the underlying graph. For instance, \frac{1}{6}\mathrm{tr}(A^3) is the number of triangles in G, or, when G is undirected, then A is symmetric and hence by the spectral theorem it has real eigenvuales \lambda_1\geq \lambda_2\geq \dots\geq \lambda_n. When G is d-regular, then \lambda_1=d, and d-\lambda_2 measures expansion properties of G which are important in several contexts.
Cons: costly in space. The space is always \Theta(|V|^2), regardless of the number of edges. This would be fine if G is dense. It is slow to add/delete a node |\Theta(|V|^2) (but is fast to add a new edge \Theta(1)).

The graph G=(V,E) is represented using an array or vector of lists. We use an array or vector L such that for a vertex u\in V, L[u] points to a list of the vertices v\in V which are adjacent to u, or a list of the edges incident to u.

For directed graphs, we will have the list of the successors of a vertex u, for all vertices u, and, possibly, the list of predecessors of a vertex u, for all vertices u.

Pro: require space \Theta(|V|+|E|), i.e. linear in the size of the graph. Moreover, they are easy to modify/implement.
Cons: Queries like whether there is an edge from vertex u to vertex v are not efficient and might require time complexity \Theta(|V|) (depending on the graph stored). An adjacency list might not suitable when the graph is dense or to compute algebraic invariants of graphs.

In many problems we deal with finite subgraphs of the integer lattice on \mathbb Z^2. Where each vertex (i, j) is connected to either four neighbors (up, left, down, right), or to eight neighbors (as before + in diagonal), or to six neighbors (hexagonal tiling), … E is a subset of all the connections.

G[i][j] indicates whether the vertex (i, j) \in V or not.

Depth-First Search

In a Depth-First Search (DFS) of a graph G=(V,E) we visit a vertex v and from there we traverse, recursively, each non-visited vertex wwhich is adjacent/a successor of v. When we visit a vertex u we say the vertex is open; it remains open until the recursive traversal of all its adjacent/successors has been finished, then u gets closed.

A basic DFS implementation

#include<vector>
#include<stack>// only needed for the iterative implementation

using namespace std;

using graph = vector<vector<int>>;
using vertex = int;

void DFS_rec (const graph& G, vertex u, vector<bool>& visited) {
    // recursive implementation
    // DFS visit of the connected component of u in G
    if (not visited[u]) {
        visited[u] = true;
        // here we might want to "visit" u
        for (auto neighbor : G[u])
            DFS_rec(G, neighbor, visited);
    }
}

void DFS_ite (const graph& G, vertex u) {
    // iterative implementation
    // DFS visit of the connected component of u in G
    int n = G.size();
    stack<int> S;
    vector<bool> visited(n, false);
    S.push(u);
    while (not S.empty()) {
        vertex v = S.top(); 
        S.pop();
        if (not visited[v]) {
            visited[v] = true; 
            // here we might want to "visit" u
            for (auto neighbor : G[v])
                S.push(neighbor);
        } 
    } 
}

A variation of DFS to detect cycles

using namespace std;

using graph = vector< vector<int>>;
using vertex = int;

void DFS_cycles(const graph& G, vertex v, vertex father, vector<bool>& visited) {
    // when calling this in the main take v as father
    visited[v] = true;
    for(auto neighbor : G[v]) {
        if (not visited[neighbor]) {
            DFS_cycles(G, neighbor, v, visited);
        } else {
            if (neighbor != father) { 
                // in here we've found a cycle! 
            }
        }
    }
}

The time complexity of DFS is linear in the size of the graph \Theta(|V|+|E|), under the assumption that the work done visiting a vertex is \Theta(1).

See an animation of a DFS run!

Jutge exercises

The exercises that can be thought as variations on Depth-First Search (DFS) are the following:

Suggested workflow

Once you have chosen a problem to solve, download the .zip archive of the problem and unzip it. In the obtained folder there are:

a file .pdf with the official problem statement
one or more text files with examples of input sample.inp
the corresponding correct outputs sample.cor

Step 1: Getting the C++ code to compile

After creating a C++ source file to solve the problem, compile it with g++ -std=c++11.

Common error(s)

Not using the flag -std=c++11.

Possible useful flags are -Wall -Wextra -Wno-overflow -Wpedantic -Werror -D_GLIBCXX_DEBUG

Step 2: Testing testing testing

Test the executable file obtained on the given example(s), for instance with ./a.out < sample.inp > output. Also, test your code against simple/trivial inputs, e.g. a graph with no-edges.

Common error(s)

Writing the input by hand.
Not checking the exact formatting of the output.

To see whether the output is the same as sample.cor a way is to use diff output sample.cor

Step 3: Submitting the solution to the Jutge

Once the code compiles and on the given samples it gives the correct output submit it to the Jutge for automatic evaluation.

Common error(s)

Sending to the Jutge code that was not even compiled locally.
Not checking if the output was correct on the given inputs.

Step 4: I’m stuck. What can I do?

You are “stuck” on a problem if you spent around 1 hour trying to solve it but still the Jutge is rejecting your solution.

Possible approaches to getting “un-stuck” are:

do not think about that problem for some time and come back to your code with fresh eyes
look again at the theory
try to explain your code to another student
ask for hints, e.g. by email. Be specific on the type of help you need. Include in the email the code of your approach.

From this block of exercises, in class we solve together the ones marked with 🔶. They are the same as the one listed below.¹

Forest

Treasures in a map (1)

Breadth-First Search

In a Breadth-First Search (BFS) of a graph G=(V,E) starting from some vertex s we visit all vertices in the connected component of s in increasing distance from s.

When a vertex is visited, all its adjacent non-visited vertices are put into a list of vertices yet to be visited.

In BFS we keep a queue of vertices that have been not yet visited. All the vertices in the queue are at distance d or d+ 1 from the starting vertex s, where d is the distance to s of the last visited vertex. Moreover, all vertices at distance d in the queue precede the vertices at distance d + 1, and all vertices of G at distance d from s have already been visited or they are in the queue. The BFS thus visits the connected component of s by traversing the levels or layers defined by the distance to s.

A basic BFS implementation

#include<vector>
#include<queue>

using namespace std;

using VI = vector<int>;
using graph = vector<vector<int>>;//to store an adjacency list of the graph
using vertex = int;

const int NOTVISITED = -1;

vector<vector<int>> bfs(const graph& G, vertex source){
    // g is a graph given as an adjacency list
    // source is a vertex in g
    // the algorithm returns a vector D. D[v] is the distance of v from source, 
    // or -1 if the v is not reachable from s
    int n = G.size();
    VI D(n, NOTVISITED);
    queue<int> pq;
    pq.push(source);
    D[source] = 0;
    while(not pq.empty()){
        vertex current = pq.front();
        pq.pop();
        // here we might want to "visit" current
        for (auto neighbor : G[current]){
                if(D[neighbor] == NOTVISITED){
                    pq.push(neighbor);
                    D[neighbor] = D[current]+1;
                }
            }
    }
    return D;
}

The time complexity of BFS is linear in the size of the graph \Theta(|V|+|E|), under the assumption that the work done visiting a vertex is \Theta(1).

See an animation of a DFS run!

Jutge exercises

The exercises that can be thought as variations on Breadth-First Search (BFS) are the following:

Suggested workflow

Once you have chosen a problem to solve, download the .zip archive of the problem and unzip it. In the obtained folder there are:

a file .pdf with the official problem statement
one or more text files with examples of input sample.inp
the corresponding correct outputs sample.cor

Step 1: Getting the C++ code to compile

After creating a C++ source file to solve the problem, compile it with g++ -std=c++11.

Common error(s)

Not using the flag -std=c++11.

Possible useful flags are -Wall -Wextra -Wno-overflow -Wpedantic -Werror -D_GLIBCXX_DEBUG

Step 2: Testing testing testing

Test the executable file obtained on the given example(s), for instance with ./a.out < sample.inp > output. Also, test your code against simple/trivial inputs, e.g. a graph with no-edges.

Common error(s)

Writing the input by hand.
Not checking the exact formatting of the output.

To see whether the output is the same as sample.cor a way is to use diff output sample.cor

Step 3: Submitting the solution to the Jutge

Once the code compiles and on the given samples it gives the correct output submit it to the Jutge for automatic evaluation.

Common error(s)

Sending to the Jutge code that was not even compiled locally.
Not checking if the output was correct on the given inputs.

Step 4: I’m stuck. What can I do?

You are “stuck” on a problem if you spent around 1 hour trying to solve it but still the Jutge is rejecting your solution.

Possible approaches to getting “un-stuck” are:

do not think about that problem for some time and come back to your code with fresh eyes
look again at the theory
try to explain your code to another student
ask for hints, e.g. by email. Be specific on the type of help you need. Include in the email the code of your approach.

From this block of exercises, in class we solve together the ones marked with 🔶. They are the same as the one listed below.²

Treasures in a map (2)

Topological Sort

A directed acyclic graph (DAG) is a directed graph that contains no cycles (as its name indicates).

DAGs have many applications since they modellize well requirements and precedence. For instance, in a large complex software system, each node is a subsystem and each arc (A,B) indicates that subsystem A uses subsystem B. Vertices with no predecessors are called roots; vertices with no successors are called leaves of the DAG.

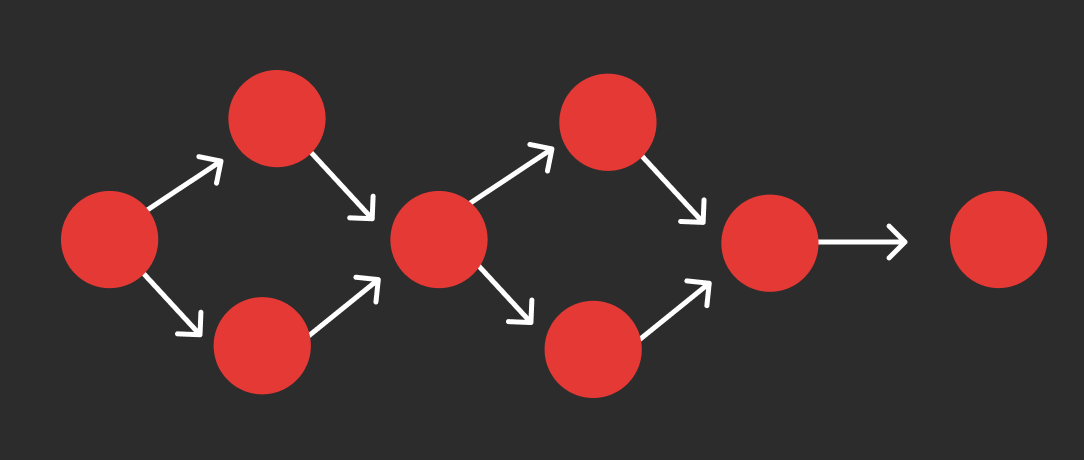
A special type of traversal that makes sense in a DAG is a topological sort. A topological sort of a DAG G=(V,E) is a sequence of all its vertices such that for any vertex w, if v precedes w in the sequence then (w,v) \notin E. In other words, no vertex is visited until all its predecessors have been visited.

Suppose that we have computed \mathsf{pred}[v], the number of predecessors of v in G that have not yet been visited. Then, if any vertex v has \mathsf{pred}[v] = 0 we can visit it and decrement by one \mathsf{pred}[w], for all its successors w. The algorithm has thus two steps:

Compute the number of predecessors \mathsf{pred}[v] for all vertices v\in G;
Repeatedly, until all vertices have been visited, visit a vertex v and update \mathsf{pred}[w] for all its successors.

See an animation of a Topological Sort run!

Jutge exercises

The exercises that can be thought as variations on Topological Sort are the following:

Suggested workflow

Once you have chosen a problem to solve, download the .zip archive of the problem and unzip it. In the obtained folder there are:

a file .pdf with the official problem statement
one or more text files with examples of input sample.inp
the corresponding correct outputs sample.cor

Step 1: Getting the C++ code to compile

After creating a C++ source file to solve the problem, compile it with g++ -std=c++11.

Common error(s)

Not using the flag -std=c++11.

Possible useful flags are -Wall -Wextra -Wno-overflow -Wpedantic -Werror -D_GLIBCXX_DEBUG

Step 2: Testing testing testing

Test the executable file obtained on the given example(s), for instance with ./a.out < sample.inp > output. Also, test your code against simple/trivial inputs, e.g. a graph with no-edges.

Common error(s)

Writing the input by hand.
Not checking the exact formatting of the output.

To see whether the output is the same as sample.cor a way is to use diff output sample.cor

Step 3: Submitting the solution to the Jutge

Once the code compiles and on the given samples it gives the correct output submit it to the Jutge for automatic evaluation.

Common error(s)

Sending to the Jutge code that was not even compiled locally.
Not checking if the output was correct on the given inputs.

Step 4: I’m stuck. What can I do?

You are “stuck” on a problem if you spent around 1 hour trying to solve it but still the Jutge is rejecting your solution.

Possible approaches to getting “un-stuck” are:

do not think about that problem for some time and come back to your code with fresh eyes
look again at the theory
try to explain your code to another student
ask for hints, e.g. by email. Be specific on the type of help you need. Include in the email the code of your approach.

From this block of exercises, in class we solve together the ones marked with 🔶. They are the same as the one listed below.³

Topological sort

Remember that for any doubt on the exercises you can ask me by email too until 6 days before the lab exam.

Footnotes

Recall that ❗ marks possibly harder problems.↩︎
Recall that ❗ marks possibly harder problems.↩︎
Recall that ❗ marks possibly harder problems.↩︎